

Next: First-order validity
Up: Week 5: First-order tableau
Previous: Week 5: First-order tableau
First-order tableaux
Prove each of the following (where
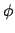
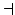
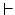
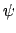 iff
iff
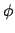
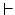
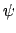 and
and
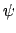
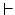
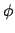 ):
):
-
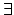 x[Fx
x[Fx 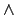
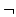 Fx]
Fx] 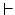
-
[
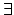 xFx
xFx 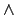
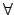 x
x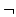 Fx]
Fx] 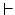
-
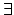 x
x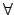 y[Rxy
y[Rxy 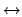
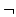 Ryy]
Ryy] 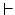
-
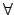 xFx
xFx 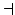
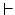
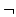
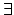 x
x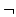 Fx
Fx
-
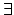 xFx
xFx 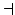
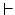
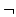
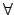 x
x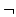 Fx
Fx
-
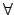 x[
x[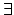 yFxy
yFxy 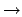 Gx]
Gx] 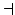
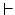
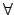 x
x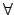 y[Fxy
y[Fxy 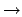 Gx]
Gx]
-
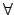 x
x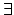 y[Fax
y[Fax 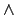 Gay]
Gay] 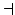
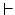
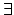 y
y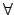 x[Fax
x[Fax 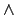 Gay]
Gay]
Sandy Berkovski
![]()
![]()
![]()
![]() iff
iff
![]()
![]()
![]() and
and
![]()
![]()
![]() ):
):