

Next: Advanced topics
Up: Week 4: Quantifiers etc.
Previous: Symbolisation II
Show that the following sets of sentences are inconsistent by
producing a set of inconsistent Herbrand sentences:
-
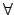 x[x smokes
x[x smokes 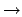
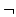 x is wise],
x is wise],
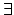 x[x smokes
x[x smokes 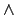 x is wise].
x is wise].
-
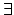 x
x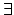 y[x hates y],
y[x hates y],
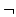
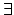 y
y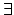 x[x hates y],
x[x hates y],
-
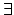 x
x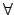 y[x hates y],
y[x hates y],
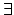 y
y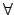 x[
x[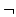 x hates y],
x hates y],
Sandy Berkovski